Max Temperature for State of the Art Rankin Cycles

Introduction

With the current aim of energy saving in society to reduce emission and attempt to diminish environmental impact of procedure and manufacturing constitute, energy recovery from industrial processes is condign a major topic. For instance, information technology was estimated that the "energy wasted by all U.S. industrial facilities could produce ability equivalent to 20% of U.S. electricity generation capacity, without burning any fossil fuel, and could assist many industries to meet contempo global warming regulation" (Sami, 2010), as a proof of how much potential rut recovery may have. In addition, given the target of reducing about 20% the emission of the European union countries, increasing efficiency and heat recovery from industrial processes volition be crucial. A study carried out by Campana et al. (2013) found that energy coming from waste heat conversion could be upwards to 2% of the European Industry energy use, leading to a substantial decrease in greenhouse gases (GHG). The industrial sectors of about concern for waste heat recovery are the ones producing cement, steel, and other metal alloys. Aluminum manufacturing plants need a large amount of electricity for their production process, with about half of the energy lost equally rut (Ladam et al., 2011). The aluminum industry world's average power consumption was 13.4 kWh/kg_Al produced as of 2017 (World Aluminium Website of the International Aluminium Constitute, 2019). Because the total amount of aluminum produced in the world, 63.4 millions metric tons (63.4 billions kg) in 2017 (World Aluminium Website of the International Aluminium Found, 2019), the heat recovery potential is vast. Ladam et al. (2011) approximate that 0.9 kWh of electric energy per kilogram of aluminum can be generated with heat recovery cycles exploiting the rut available at the cathode (to a higher place 300°C pot shell temperature), anode, and the pot flue gas (120–160°C with current technology but an increase is expected with near-hereafter technologies). Current and future technology evolution on the electrolysis procedure will lead to lower power consumption. Today's state of the art is effectually 12 kWh/kg_Al with a target of ten kWh/kg_Al (Solheim, 2018). In gild to achieve such depression targets, lower pot vanquish temperatures (eastward.g., 250°C) and recovery of estrus from the electrolysis cells may exist essential (Solheim, 2018).

Given the estrus source temperatures and relatively modest size of the heat recovery Rankine cycle, organic fluids are expected to outperform steam as working fluid (Cavallini, 2017). Karellas et al. (2013) investigated waste estrus recovery cycles for the cement industry, finding that, if the frazzle gas temperature is below 310°C, the organic Rankine wheel (ORC) is more than efficient than the steam cycle. Zhang et al. (2013) compared ORC, steam bicycle, and cascaded steam-organic cycle options for estrus recovery from steel plants. For frazzle gas temperatures betwixt 200 and 300°C, the all-time option found was an ORC with R141b equally working fluid. As far every bit aluminum production plants are concerned, recently, Yu et al. (2018) assessed the functioning of heat recovery ORCs for an aluminum product establish located in Iceland wasting about 88 MW of thermal power from the smelter exhaust gases.

In this work, a hereafter aluminum constitute case study, based on Norwegian conditions, is selected to evaluate the benefits of estrus recovery. The plant features 2 hot streams at different temperatures: one stream from the cooling medium of the pot jail cell walls (cathode) and one from the pot flue gases. The objective of the work is to place the optimal ORC design [working fluid, pressures, temperatures, mass period rates, layout, and oestrus exchanger network (HEN)] besides as the energy and economic performance with state-of-the-art computer-aided tools. The master peculiarity of the plant is the availability of two hot streams with different temperatures, which calls for the utilize of heat integration methodologies. For this reason, working fluid and cycle pressure and temperatures are optimized with the systematic optimization approaches recently proposed by Scaccabarozzi et al. (2018), while the ORC design, mass menses rates, and HEN are optimized with the approach developed by Martelli et al. (2017) and Elsido et al. (2018). Both approaches tin handle the optimization of Rankine cycles integrated with multiple hot and cold streams. Thanks to the use of such efficient reckoner-aided tools, the written report considers 72 pure fluids and 30 binary zeotropic mixtures, making information technology possible to compare the free energy and economic performance achievable with different fluids.

Problem Argument

The case study is a future aluminum production plant based on Norwegian atmospheric condition. The plant is based on several electrolytic reduction cells (also chosen "smelters"), which operate at high temperature (about 940–980°C) absorbing about 10 kWh/kg_Al. Information technology is assumed that in novel aluminum production processes, about 35% of the electricity is converted into heat and released with the stream of flue gases leaving the pot at about 180°C and the pot beat cooling air at approximately 250°C. Figure 1A shows a schematic menses diagram of the plant. In this study, it is assumed that the two hot streams make available the same thermal ability (near vii.8 MW each), and both tin be used every bit heat sources for a heat recovery ORC. While the pot exhaust gases must be cooled down to 80°C because of the specifications of the downstream filters, the pot cooling air tin can be cooled down to xx°C (minimum outlet temperature). Body of water water at 10°C was assumed to be available near the institute site as cold utility for the ORC condenser and to waste the unrecovered thermal ability. A summary of the stream backdrop is reported in Effigy ane. The composite bend of the 2 hot streams, which is obtained past applying the same principles of "pinch analysis" described by Linnhoff (1979) and Kemp (2006), is reported in Figure 1B. The peculiarity compared to having a single hot stream is the variation of the overall available heat capacity flow rate due to the presence of two estrus sources.

Figure i. General scheme of the case written report (A) and composite curve of the available hot process streams (B), and data for the aluminum manufacturing constitute example report.

Optimization of Working Fluid Selection

Since performing a detailed techno-economic optimization of the ORC for each possible working fluid is clearly not practicable because of the required computational time, iii classes of computationally efficient approaches take been proposed:

- Screening approaches: numerical methods are employed to select the cycle configuration and operating parameters for a set of candidate fluids, which is identified based on engineering criteria [encounter, e.one thousand., (Wang et al., 2011; Scaccabarozzi et al., 2018)];

- Figurer-aided molecular design methods [see, e.g., (Papadopoulos et al., 2010; Palma-Flores et al., 2014)]: the synthesis of the molecule of the working fluid is automatically optimized with a challenging Multiple Integer Non-Linear Programming (MINLP) problem to find the fluid with the near suitable properties; the problem can include the optimization of the cycle variables;

- Molecular targeting methods [see, e.g., (Lampe et al., 2014)]: the molecule design and properties of the ideal ("target") fluid are simultaneously optimized with the bike configuration and cycle variables; the existent working fluids with the well-nigh similar properties are identified in a second stage using an ad hoc procedure.

For a thorough review of computer-aided fluid selection and ORC design optimization methods, the reader is referred to Linke et al. (2015).

In this work, the screening approach proposed by Scaccabarozzi et al. (2018) is used. First, a set of pure fluids and binary zeotropic mixtures is identified; then, for each fluid, the maximum doable free energy performance is determined with an ad hoc optimization algorithm. Fluids are ranked in terms of energy performance, and those with the most promising combination of performance indices (including ODP, GWP, wheel operating pressures, etc.) are considered for a more detailed technoeconomic optimization study. The methodology has besides the reward of finding the values of the bicycle pressures and temperatures that maximize the efficiency. These values of wheel pressures and temperatures tin exist passed as input data to the technoeconomic optimization methodology (run across Technoeconomic Optimization).

Set of Candidate Fluids

The complete list of pure fluids and mixtures considered in this work is listed in Tabular array 1. Differently from Scaccabarozzi et al. (2018), nearly all the pure working fluids available in REFerence fluid Backdrop REFPROP v9.1 (REFerence fluid PROPerties) take been considered. Fluids that are flammable and/or with positive ODP and/or high GWP are also included with the aim of comparison them with newer alternatives. Only fluids with besides low critical temperatures (i.east., 50°C) and/or thermal stability beneath 200°C accept been discarded. Fluids with unknown thermal stability limits take been included in the analysis with the objective of assessing the achievable performance and guiding time to come research efforts: if they turn out to be promising, their thermochemical stability limits tin be adamant with time to come ad hoc experimental campaigns [every bit washed in (Invernizzi et al., 2016)]. Every bit far as mixtures are concerned, given the big number of possible combinations of fluids, it is necessary to perform a preliminary screening. On the basis of the results of Scaccabarozzi et al. (2018), for a similar waste heat recovery application, the nigh promising binary zeotropic mixtures feature a critical temperature within 250 and 500°C and an appreciable temperature glide (>5°C) in condensation (with condensation pressures evaluated ranging from 0.05 to 5.05 bar). Mixtures proposed in previous studies have been included as well. It is important to observe that for 24 mixtures denoted in Table A2, due to the lack of experimental information to calibrate the equation of states, REFPROP estimates the thermodynamic properties with the full general arroyo proposed in Lemmon and McLinden (2001).

Table 1. List of the pure fluids and mixtures considered in this report.

Thermodynamic Optimization Methodology

Given the fix of available hot and cold streams of the establish, for each candidate working fluid (pure fluids and/or mixtures), the algorithm of Scaccabarozzi et al. (2018), which was adopted for this study, can determine the cycle pressure, temperature, and mass menstruation rates, which maximize a relevant energy performance index. For oestrus recovery applications, the virtually appropriate free energy functioning alphabetize is the net power generated by the ORC or, equivalently, the exergy efficiency (Scaccabarozzi et al., 2018):

$\begin{array}{ll}{\eta }_{\text{ex}}=\frac{{\dot{W}}_{\text{ORC}}}{{\dot{\text{Q}}}_{\text{H}1}\left(\mathrm{one}-\frac{T_0}{T_{\text{ML},\text{H}1}}\right)+{\dot{\text{Q}}}_{\text{H}2}\left(1-\frac{T_0}{T_{\text{ML},\text{H}2}}\right)}& (1)\end{array}$

Where Ẇ _ORC is the internet ORC ability output, $\stackrel{\bullet }{Q}$ is the thermal ability of the hot stream and T _ML denotes the hateful logarithmic temperature between the hot stream inlet and outlet temperatures and T ₀ is the dead country (ambience) temperature. Some other suitable performance index is the first law efficiency, defined every bit follows:

$\begin{array}{ll}{\eta }_I=\frac{{\dot{W}}_{\text{ORC}}}{{\dot{\text{Q}}}_{\text{H1}}\text{+}{\dot{\text{Q}}}_{\text{H2}}}& (2)\end{array}$

Since the denominator of Equation (1) and (2) are problem data, maximizing Ẇ _ORC, η _ex or η _I is equivalent. In this study Equation (1) was chosen equally objective function of the optimization problem.

The methodology (Scaccabarozzi et al., 2018) combines the evolutionary algorithm PGS-COM (Particle Generating Fix-Circuitous algorithm) (Martelli and Amaldi, 2013) with the well-known energy targeting methodology of Kalitventzeff and Maréchal (1999). The cake-period diagram of the algorithm is shown in Figure two.

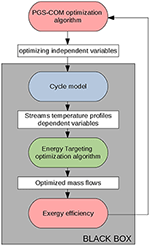
Effigy 2. Block-flow diagram of the algorithm.

The evolutionary algorithm PGS-COM optimizes the independent cycle variables, namely, the evaporating and condensing pressure, the turbine inlet temperature, and the mixture composition. Each combination of independent cycle variables sampled past PGS-COM is given as input to the blackness-box, which solves the cycle model to calculate the dependent variables (east.m., streams temperature profiles, mass catamenia rates, etc.) and the objective function (2nd constabulary efficiency).

In the black-box, the ORC model is implemented in Matlab^® R2015 (The MathWorks Inc, 2015). All the intensive and specific backdrop of the bicycle streams, such equally the temperatures, pressures, and enthalpies are calculated with REFPROP v9.i (Lemmon et al., 2013), for both pure fluids and mixtures. The bike model checks also whether the following constraints of the wheel optimization problem are met:

• Vapor fraction of the flow evolving in the expander greater or equal to 0.88;

• Temperature difference in the heat exchangers ≥ five°C;

• Condensation pressure level ≥ 0.03 bar.

These constraints are handled within PGS-COM with the extreme barrier approach (see Astolfi et al., 2017). Since the methodology must screen a large number of working fluids, the ideal Rankine cycle is considered in the assessment of the performance (i.e., isentropic pump and turbine, and heat exchangers without pressure drops and oestrus losses) so as to save computational time compared to more sophisticated models.

One time all the cycle-specific and intensive properties are adamant, only the mass period rates of the ORC and cooling water are missing. The estrus integration between ORC streams and rut sources/oestrus sinks is optimized with the methodology proposed by Kalitventzeff and Maréchal (1999), which determines the maximum mass flow charge per unit of the working fluid that can exist generated (the so-chosen "maximum heat recovery target"), and therefore the maximum cycle net power, for a given minimum allowed heat transfer temperature difference. The associated linear plan can be formulated as follows:

$\begin{array}{l}\text{subject field to}:\\ A\mathrm{10}=b& (\mathrm{four})\end{array}$

where x denotes the vector of decision variables (including ORC mass period rate, cooling water mass flow rate and heat cascade residual heat flows), Equation (4) denotes the linear system of equations of the oestrus cascade (i.e., heat balance of each temperature interval) (Linnhoff, 1979; Kemp, 2006), and w is the vector of net specific works associated to each utility mass catamenia rate (ORC and cooling h2o). The linear program defined past Equations 3 through 5 features N − 1 + K variables and N constraints, where N denotes the number of temperature intervals and M is the number of utilities with unknown mass flow rates (two for our example). Compared to the plain rut pour arroyo for streams featuring constant estrus chapters, nosotros considered 300 intervals so as to closely approximate the temperature profiles of supercritical working fluids (in each interval, the rut capacity variation is negligible). The linear program is solved in Matlab^® with the default algorithm of the "linprog" function in <1 southward.

For each fluid, the average total computational time to reach convergence of the PGS-COM algorithm is approximately xxx min, corresponding to about ii,000 function evaluations.

Fluid Ranking and Selection

Tables 2, 3 report the results of the thermodynamic optimization for the first x pure fluids and mixtures, respectively, whose thermodynamic properties were all evaluated by means of REFPROP v9.one. The complete ranking of fluids is reported in Table A1 and Table A2 in the Appendix. The pure fluid leading to the highest exergy efficiency (and net ability output) is RE347mcc, a hydrofluoroether, with GWP = 530. The maximum recoverable electric power is 3530.63 kW. The other nine fluids are either combustible (Neopentane, Butane, Isobutene, ane-Butene, Propylene) or with positive ODP (R114, R115) or with high GWP (R143, R245fa2). The starting time non-flammable fluid with zilch ODP and almost-zero GWP is R1336mzz, ranked 16th in terms of exergy efficiency. Using such fluid, the maximum recoverable power output is only 3.5% lower than the first one (RE347mcc). Slightly lower efficiency can be reached using R1233zde, another non-flammable fluid with naught ODP and almost-zippo GWP, which ranks 23rd.

Table 2. List of the 10 all-time performing pure fluids.

Table three. Listing of the ten best performing mixtures.

Similar to what was done by Scaccabarozzi et al. (2018), who plotted the second law efficiency accomplished with each working fluid against the ratio between its critical temperature and the inlet temperature of the hottest oestrus source, Effigy 3A shows that there is an evident relation betwixt the maximum achievable efficiency and the already mentioned temperature ratio. Specifically, fluids with a critical temperature either in the range 66–69 or 81–84% of the maximum estrus source temperature (i.due east., 523.15 K) are those ones that show highest efficiency. The former group of fluids (namely, R115, R143a, and propylene) exploits supercritical turbine inlet pressures while the latter features pressures close to the critical i (slightly subcritical or supercritical). On the other hand, the critical temperature is not the unique fluid property affecting the maximum achievable efficiency. Indeed, although RE347mcc and R1233zde have a negligible difference in critical temperatures (about ane°C), the exergy efficiency is appreciably unlike (85.3% vs. 81.3%), indicating that the critical temperature is the fluid property with the major consequence on cycle efficiency, simply in that location are other relevant thermodynamic properties. Such properties are those which control the shape of the saturation curve in the temperature–entropy (T–southward) diagram, mainly the liquid specific heat capacity and the molecular complication (influencing the slope of the saturated vapor line) (Invernizzi, 2013). These properties influence not only the efficiency of the thermodynamic cycle but as well the oestrus integration with the available hot and cold streams of the procedure (i.e., pinch indicate positions and heat recovery factor), as shown in the composite curves of Figures 4A,B. Information technology is worth noting that the composite curves include the hot and cold streams of the ORC in addition to the hot procedure streams (H1, H2) and the cooling water (i.east., the cold curve is made past the cooling water, economizer, evaporator, and superheater of the ORC, while the hot curve is fabricated by H1, H2, ORC desuperheater, and condenser). For case, the composite curve of the cycle using RE347mcc features a very small heat transfer temperature divergence from 150 to 30°C. Surprisingly, in the optimized oestrus integration solution, the ORC regenerator is used to compensate for the relative reduction of process heat below 80°C (as the stream of exhaust gases beneath eighty°C).

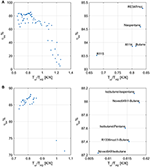
Figure three. Exergy efficiency of the considered pure fluids (A) and mixtures (B) every bit a function of the ratio betwixt their critical temperature and the inlet temperature of the hottest source.

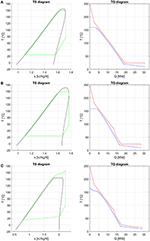
Figure 4. Temperature–entropy (T–s) diagram and blended curves (T–Q diagrams) of the optimized organic Rankine wheel (ORC) employing RE347mcc (A), R1336mzz (B), and the binary zeotropic mixture isobutane/isopentane (0.66/0.34) (C). The saturation curve of this last ane could not be computed in a reliable way in the region close to the critical temperature due to convergence issues of the wink calculation.

Equally far as mixtures are concerned, the best zeotropic mixture (in terms of energy efficiency) is isobutane (66% mass ground)–isopentane (34%), leading to an exergy efficiency gain of about 2.8 percentage points with respect to the best pure fluid. The corresponding increase in net power output of the ORC is 3.iii%. The optimal bicycle is supercritical for the first 10 mixtures, except for the 6th and seventh (butane/pentane, isopentane/R245fa). Unfortunately, all the mixtures in the first positions comprise a high concentration of hydrocarbons, which may lead to safe issues related to fluid flammability. Figure 3B shows the relation between the maximum achievable exergy efficiency and the critical temperature of the mixture. It indicates that the mixtures with the highest exergy efficiency accept a critical temperature lying in the range 80–82% of the maximum oestrus source temperature. Figure 4C shows the T–south and composite curves (temperature–heat) diagrams for the first mixture. Compared to pure fluids, the condensation temperature glide (nearly 10°C) reduces the irreversibility (exergy loss) occurring in the heat transfer process between the condensing fluid and the cooling water. Furthermore, the mixture features also a ameliorate matching at loftier temperatures with the hot process stream thanks to the supercritical cycle configuration.

Given the results of the thermodynamic optimization, the condom issues of flammable fluids and the current limitations on the ODP, HFE-RE347mcc, and HFO-R1336mzz are selected for the technoeconomic optimization. Despite its flammability, the mixture isobutene/isopentane is likewise considered in the technoeconomic optimization with the goal of assessing the potential economic advantage of using zeotropic mixtures compared to pure fluids.

Technoeconomic Optimization

The pure fluids and the mixture selected in Fluid Ranking and Pick are compared from a technoeconomic indicate of view, keeping the cycle parameters (i.e., wheel pressures and temperatures) stock-still at the optimal values found in thermodynamic optimization. The goal of the technoeconomic optimization is to determine the all-time merchandise-off between free energy efficiency and capital costs of the ORC and the heat exchanger network (HEN). To the best of the authors' knowledge, the problem of the technoeconomic optimization of the design of the integrated HEN and ORC has been addressed but by few works in literature. Desai and Bandyopadhyay (2009) were the first authors to consider process integration of ORCs for waste material heat recovery. They causeless fixed ORC schemes (i.e., with turbine haemorrhage and regeneration) and imposed that the ORC tin apply the depression-temperature heat below the process compression bespeak; only later determining the operating weather of the ORC are heuristics employed to derive a feasible HEN. Chen et al. (2016) evaluated the employ of an intermediate estrus transfer fluid or the direct integration of ORC and estrus sources/sinks with an optimization method. They solved the heat integration problem with the objective to maximize the net power output of the ORC. The economic feasibility of the solutions is considered simply afterward the optimization. Hipólito-Valencia et al. (2013) proposed a method to simultaneously optimize the design of HEN and ORC based on 2 simplifying assumptions: they assumed fixed ORC schemes and considered a limited fix of fixed rut integration options between ORC streams and heat sources/sinks. Yu et al. (2017) addressed the problem of technoeconomic ORC optimization for waste heat recovery from multiple streams. For safety and controllability reasons, they only considered indirect integration with hot water equally an intermediate heat transfer fluid between estrus sources/sinks and ORC. The well-known energy targeting model proposed past Duran and Grossmann (1986) is used to accost the heat integration, and then a suboptimal HEN is derived heuristically.

Martelli et al. (2016, 2017), and Elsido et al. (2017a,b) proposed a simultaneous method for the combined synthesis of HENs and utility systems for one or more bachelor heat sources, including heat recovery cycles, and the selection and pattern of the latter ones, while because all the possible integration options between procedure rut sources/sinks and utility systems. Compared to sequential or separated approaches, the advantage of the simultaneous approach is that it allows one to systematically optimize not merely the bicycle configuration but also the oestrus integration and HEN while rigorously taking into business relationship the trade-off between energy efficiency and costs. For this reason, the methodology proposed by Martelli et al. (2017) has been selected for this work.

Technoeconomic Optimization Methodology

The method proposed by Martelli et al. (2017) is based on the use of the general "p-h superstructure" for Rankine cycles (such as steam cycles, ORCs, and oestrus pump cycles) (Elsido et al., 2017a) and the extension of the SYNHEAT (Yee and Grossmann, 1990) superstructure for HEN design, able to generate a very wide diversity of possible matches betwixt process streams and utility streams. The ORC streams in the superstructure are characterized with variable mass period rate and binary variables for their selection. Thanks to the combination of the 2 superstructures, the methodology allows one to configure and optimally design the ORC and HEN simultaneously, integrate the heat sources/sinks with the cycle, while considering energy efficiency and capital costs (i.due east., targeting the minimum total annual toll, rather than simply efficiency). A scheme of the extended superstructure for ORC and HEN design is shown in Figure v. In this work, since but single force per unit area level ORC designs are considered, all the stream mass menstruation rates of the ORC can exist represented with a unmarried activation variable y _ORC and mass flow rate ṁ _ORC .

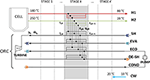
Effigy 5. Scheme of the combined HEN + ORC superstructure for techno-economic optimization. Hot and common cold streams are represented with arrows pointing respectively to the right and to the left. In temperature stage k, all the possible rut exchangers between hot stream i and cold stream j in phase thousand, that tin be selected with binary variables (z _ijk ), are represented with black vertical connectors. In addition, each ORC stream u is characterized by variable mass period rate ṁ _u and a binary variable for its selection y _u .

The mathematical model is characterized past the following variables, constraints, and objective function.

Decision Variables

• Heat exchanged between each hot stream and each common cold stream (process, ORC, and cooling water streams) in each temperature stage of the HEN (positive continuous variables),

• Temperature of each hot and cold non-isothermal stream at hot end of each phase (continuous variables),

• Temperature difference for each heat exchanger between each hot and cold stream at hot end of each stage (positive continuous variables),

• Activation of the estrus exchanger betwixt each hot stream and each cold stream in each phase (binary selection variables),

• Area of the estrus exchanger betwixt each hot stream and each cold stream in each stage (positive continuous variables),

• Activation of each ORC stream (binary selection variables),

• Mass menstruation rate of each ORC stream (positive continuous variables).

Constraints

• Overall energy balances for all hot and common cold streams in the HEN,

• Phase energy balances for all hot and cold streams in the HEN,

• Monotonicity of temperature profiles of streams along the stages,

• Logical constraints relating the heat exchanger load and expanse with the corresponding binary variables for the selection of the heat exchangers, for all possible matches between hot and cold streams,

• Logical constraints relating the continuous variables representing the mass catamenia rate for all streams of the ORC and the respective binary variables for the selection of the streams,

• Boosted logical constraints relating the existence of ORC streams with the beingness of all possible heat exchangers involving them,

• Mass and energy balances at each header of the p-h superstructure,

• Constraints to calculate the temperature differences for the selected heat exchangers,

• Relation between heat exchanger areas, hateful logarithmic temperature differences, global heat transfer coefficient, and heat duty of the heat exchanger.

Objective Function

The not-linear objective role to exist minimized is the full annual toll (TAC) of the overall HEN and ORC, which includes the sum of the investment costs for the HEN, for the ORC, the operational costs due to cooling water pumping and auxiliaries' consumption, and the avoided costs for buying the produced electricity from the filigree at the wholesale price:

$\begin{array}{l}\min TAC=CCRMF(C_S{S}_{REF}{\left(\frac{{\dot{m}}_{ORC}\Delta h_T{\eta }_{ME,T}}{S_{R\mathrm{Eastward}F}}\right)}^{\alpha }\\ +{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{k\in K}{C}_A}}}{A}_{REF}{\left(\frac{A_{ij\mathrm{1000}}}{A_{REF}}\right)}^{\beta }\\ +{\displaystyle \sum _{i\in I}{C}_A}{A}_{R\mathrm{Eastward}F}{\left(\frac{A_{CW,i}}{A_{R\mathrm{Eastward}F}}\right)}^{\beta })+{\displaystyle \sum _{i\in I}{C}_{CW}}{q}_{CW,i}\\ -h_{EQ}{p}_{EL}\left({\dot{m}}_{ORC}\Delta h_T{\eta }_{ME,T}-{\dot{\mathrm{thousand}}}_{ORC}\Delta h_P/{\eta }_{G\mathrm{Due\; east},P}\right)& (6)\end{array}$

The variables that appear in the formula above are equally follows: ṁ _ORC which represents the mass period rates of the ORC working fluid; A _ijk and A _{CW, i} , which correspond the area of a heat exchanger between each stream i in the set I of hot streams (both procedure and ORC streams) and each stream j in the set J of cold streams or cooling h2o (CW) in each temperature phase k in the gear up Chiliad; and q _{CW, i} , which represent the heat exchanged betwixt each stream i in the prepare I of hot streams (both process and ORC streams) and the cooling h2o (CW). The cost functions of rut exchangers, utilities, and components of the Rankine bicycle are dependent on the size of the equipment according to the well-known economic system of calibration constabulary: for the area of the rut exchangers, C _A is the area-specific cost at the reference size A _REF and β is the exponent; for the ORC turbine, C _{Due south} is the specific cost at the reference size Southward _REF and α is the exponent. and are the specific enthalpy differences while η _{ME, T} and η _{ME, P} are the mechanical/electric efficiency employed to calculate the nominal power of turbine and pump, respectively. The investment costs are multiplied for the factor MF bookkeeping for installation costs, construction, contingencies, etc. So, the total plant price is annualized using the levelized annual capital letter carrying accuse charge per unit, CCR, defined by the EPRI (Electric Power Research Plant) methodology (E. P. R. Institute, 1993), which takes into business relationship the expected constitute lifetime, debt/equity ratio, corporate income taxes, owner costs, etc. The parameter p _EL represents the electricity price, and h _EQ is the number of full-load equivalent operating hours.

Every bit shown in Martelli et al. (2017), the resulting non-convex MINLP problem is very challenging. It can be effectively solved using the ad hoc bilevel decomposition method recently proposed past Elsido et al. (2018, in press). The method is based on a decomposition of the full Mixed-Integer NonLinear Programming (MINLP) problem into a master MILP problem and an Nonlinear Programming (NLP) subproblem. The master problem is a relaxed and linearized version of the original MINLP problem, combining the outer-approximation linearization technique with McCormick relaxation, valid redundant constraints, piecewise linearization of the cost functions, and "nested" integer cuts. The integer variables establish by the main problem are so fixed and used to generate the NLP subproblem. The NLP subproblem includes all the continuous variables of the full problem, and all the linear and non-linear constraints of the full trouble, with fixed integer variables plant by the master problem. The objective function is the minimization of the TAC. From the resolution of the NLP sub trouble, at each iteration, an upper bound to the objective office is found and the linearization of the main problem is updated; in improver, new integer cuts are included in the master problem. The interested reader can find the mathematical details of the algorithm in Elsido et al. (2018, in printing).

Assumptions for Technoeconomic Optimization

The chief assumptions used for the technoeconomic optimization are reported in Table iv. The outlet temperature of hot process stream H2 is assumed as variable, constrained to be ≥ 20°C. In the instance of the isobutane/isopentane (0.66/0.34) mixture, the supercritical heating has been causeless as equivalent to two transformations with constant specific heat, one between 18 and 150°C and the other between 150 and 165°C.

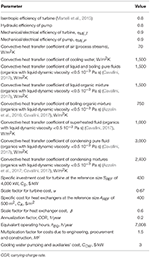
Table 4. Data for the techno-economic optimization.

2 scenarios for the technoeconomic optimization study are considered:

• Depression electricity price, p _EL equal to lxx $/MWh

• High electricity price, p _EL equal to 140 $/MWh, to account for possible financial incentives to waste product estrus recovery.

Due to large power consumption of the aluminum product process, the electricity generated by the ORC is not sold to the electrical grid only self-consumed by the establish, leading to savings in the electricity bill (i.e., it represents an avoided toll). For this reason, the economical value of electricity is representative of the average electricity purchase cost of the plant (not the electricity selling cost). The low electricity price of 70 $/MWh in this work is meant to stand for a realistic price within the next 10 years in Norway. The average electricity spot toll of the Nordpool (Nordpool, 2019) market for the Oslo area in Kingdom of norway was 50.2 $/MWh in 2018. The network cost including transmission and distribution was approximately 6.8 $/MWh to exist added to the spot price, according to ENTSO-E (European Network of Transmission System Operators for Electricity) (ENTSOE, 2019). The electricity price is expected to increment until 2030 with ~20% in Kingdom of norway, according to International Energy Agency (IEA) (IEA and Nordicetp, 2016), pregnant an electricity price of 70 $/MWh is a reasonable assumption for this work.

Due to the lack of reliable literature data, the actress equipment costs required to forestall fluid leakages and to perform fluid makeup are not considered. These additional costs are expected to exist college for the zeotropic mixture as better sealing systems are required. Indeed, as reported in Kruse and Rinne (1992), leakages may cause changes in the limerick of the working fluid (e.g., the more volatile compound may leak out more quickly than the other one), causing variations of the cycle performance. However, considering such issue requires a more detailed engineering report, which is out of the telescopic of this work.

Every bit far every bit the HEN superstructure is concerned, five temperature stages have been considered for all working fluids, yielding MINLP problems with 592 single equations, 332 continuous variables, and 73 binary variables. The computational time on a single-cadre estimator for convergence of the bilevel decomposition algorithm (Elsido et al., 2018, in printing) (i.e., no solution improvement for 20 iterations or zippo gap between upper and lower bound) is about 600–ane,800 s (20–60 iterations of the algorithm).

Results of Technoeconomic Optimization

The optimization results for the low and high electricity toll case are presented, respectively, in Tables 5, six and Figures 6, 7. The scheme of the establish using RE347mcc is shown in Figure 6A. The economizer is split into ii parallel branches heated, respectively, past H1 and H2. The heat for the evaporator is provided by H2. The scheme of the plant using the isobutane/isopentane (0.66/0.34) mixture is shown in Figure 6C. In this case, the two exchangers in serial coupled with H1 could exist merged in a single larger rut exchanger. This selection would lead to some savings in the investment toll, just it cannot be handled by the HEN synthesis methodology that assumes constant specific heat capacity within each heat exchanger. Similarly, the desuperheater and condenser in serial coupled with cooling water (i.east., in Figures 6A,B for the low electricity price case, respectively, for RE347mcc and R1336mzz, and also in Figures 7A,B for the high electricity price scenario, respectively, for RE347mcc and R1336mzz) could be merged in a single larger oestrus exchanger, just it cannot be obtained by the adopted HEN synthesis methodology.

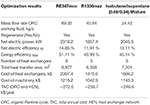
Table five. Results of the techno-economic optimization for the low electricity price scenario (70 $/MWh).

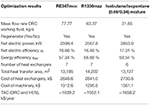
Table half-dozen. Results of the techno-economic optimization for the high electricity price scenario (140 $/MWh).

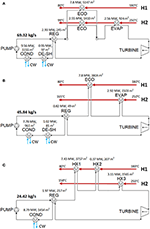
Figure 6. Optimized schemes of the optimal solutions found with fluid RE347mcc (A), R1336mzz (B), and isobutane/isopentane mixture (C) for the electricity toll equal to 70 $/MWh.

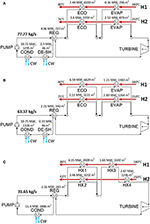
Effigy 7. Optimized schemes of the optimal solutions found with fluid RE347mcc (A), R1336mzz (B), and isobutane/isopentane (C) for the electricity cost equal to 140 $/MWh.

For all working fluids and in both price scenarios, the optimal solution found by the algorithm is a single pressure ORC bicycle with regenerator and the TAC is negative (meaning that there is an economic advantage in installing the ORC). The regenerator is used in all cases considering organic vapors (on the hot side of the regenerator) feature a oestrus transfer coefficient higher than streams H1 and H2 (air): to preheat the liquid, from an economic point of view, it is more than advantageous to use the regenerator instead of the economizers. In the low electricity cost case, the bike using RE347mcc achieves the best efficiency and economical performance, with internet electric power output equal to 2316.two kW (−34% compared to the ideal target) and TAC equal to −272.5 1000$/year (being negative, it is a revenue). The divergence in electric ability output between the economic optimization solution and the thermodynamic target is due to i) the expansion losses in the existent cycle turbine featuring an isentropic efficiency equal to eighty% and 2) the decrease of oestrus recovered from the heat sources. Apropos the final betoken, the economically optimal solution has −13.5% working fluid mass flow rate compared to the target establish with the thermodynamic optimization owing to the need of containing the investment cost of the heat exchangers. Compared to RE347mcc, the economical profit of the solutions obtained using R1366mzz and the isobutane/isopentane mixture is −15.1 and −9.5%, respectively. The master reason appears to exist the lower working fluid mass menstruation charge per unit (25–28% lower than the target), which limits the net electrical power output (−24.7 and −11.7%, respectively, compared to RE347mcc). Interestingly, the reduction of mass period rate compared to the thermodynamic target is about double of that found for RE347mcc (−13.5%). This is due to (1) pinch indicate at the evaporator, which limits the working fluid mass flow rate, and (2) plush recovery of low-temperature oestrus from estrus source H2. Concerning the evaporator, in the depression electricity price scenario, there is no evaporator coupled with rut source H1 (or the high-temperature heat exchanger in the example of the mixture) in any of the three fluids, considering information technology would be highly expensive due to the low heat transfer coefficient of the hot stream and the small-scale temperature difference (stream H1 has an inlet temperature quite close to the evaporation temperatures). Therefore, the mass flow rate of fluid that can be evaporated is express by the heat of H2 available from 250°C to the pinch point with the evaporation temperature (or critical temperature in case of supercritical fluid). RE347mcc has a smaller enthalpy of evaporation (equal to 36.95 kJ/kg) compared to R1336mzz (63.65 kJ/kg), and this allows the generation of a larger mass flow rate of vapor using simply the heat available for the evaporator in H2. For R1336mzz, the mass menstruation rate of generated vapor is limited by the heat available in H2 for evaporation, and this causes a considerable reduction of heat recovery compared to the thermodynamic optimization. The ORC using the mixture shares the aforementioned issue as R1336mzz because of the large heat chapters of the supercritical fluid around the disquisitional temperature (between 150 and 165°C), equal to 143 kJ/kg. For R1336mzz and the mixture given the limited mass menstruation rate of working fluid raised by the evaporator (for the mixture, the high-temperature heat exchanger HX3), information technology is sufficient to use the regenerator and the economizer in H1 for liquid preheating. For RE347mcc, given the larger mass flow rate of fluid, another economizer is necessary to preheat the liquid recovering heat from H2 leading to a higher oestrus recovery charge per unit compared to the other two fluids (this is evident looking at the outlet temperatures of stream H2 reported in Figures 6A–C).

For the scenario with loftier electricity prices (e.m., the constitute benefits from incentives), the corporeality of recovered heat and the mass flow rate of working fluids are very close to the thermodynamic target. As already pointed out by Elsido et al. (2019) in a similar analysis, since the electricity revenues more than compensate for the investment toll, the energy functioning has the major weight on the plant full almanac cost (or cyberspace present value). Consequently, the economic optimum lies close to the thermodynamic 1. Compared to the solutions found for the depression electricity price, the HENs of the solutions institute for the high electricity toll scenario utilize one more rut exchanger for RE347mcc and the mixture, and two more heat exchangers for R1336mzz (see Figures 7A–C). The cost of the HENs increases by +31% (RE347mcc), +62% (isobutane/isopentane mixture), and +92.5% (R1336mzz) with respect to the depression electricity price solutions. Every bit far as the economical functioning is concerned, the cycles using RE347mcc and the isobutane/isopentane mixture achieve the best economical operation, an annualized net turn a profit of nearly 1.65 One thousand$/yr, with a negligible (i%) divergence. The ORC using R1336mzz features similar power output to RE347mcc, but its TAC is mainly penalized past the higher heat exchanger costs (+7.3%). Due to the small availability of vapor desuperheating heat, the regenerator gives only a marginal contribution and liquid economization needs to exist performed to recover low temperature heat from H1 and (especially) H2, which features a very poor heat transfer coefficient. In comparing, the cycles with R347mcc and the mixture tin can preheat more the liquid with the regenerator and save some heat transfer expanse of the economizers. This is articulate from the comparison of the solutions obtained for RE347mcc and R1336mzz (see Figures 7A,B): the ORC configuration and the HEN scheme are the same for the two fluids, likewise equally the corporeality of heat recovered from the estrus sources (the outlet temperature of H2 is equal to 75–76°C in the ii cases), simply the amount of rut exchanged in the regenerator for the case using RE347mcc is 84% larger than in the case employing R1336mzz. Therefore, the overall HEN cost of the latter is 7.iii% larger than the heat exchangers price of the case with RE347mcc, leading to a worse economic operation.

Conclusions

For both pure fluids and mixtures, in that location is clear relation between the maximum achievable exergy efficiency and the critical temperature. The fluids achieving the highest efficiency feature a critical temperature in the range lxxx–84% of the maximum estrus source temperature. The maximum efficiency cycle turns out to take a turbine inlet pressure close to the disquisitional ane. Every bit an exception, R115, R143a, and propylene attain close to maximum efficiency employing a highly supercritical turbine inlet pressure (their disquisitional temperature is only 66–69% of the maximum rut source temperature).

The offset ranked pure fluid is RE347mcc, which can reach an exergy efficiency of 85.28% (corresponding to an ORC net power target of 3.53 MW) with a subcritical regenerated ORC. It appears to be a promising candidate since it is non-flammable, its ODP is zero, and the GWP is not excessive (530). If flammable fluids are discarded considering of safety issues, the about promising alternatives seem to be R1336mzz (GWP = two) and R1233zde (GWP = 1). In all solutions, the regenerator of the ORC is used to compensate for the relative scarcity of available estrus below fourscore°C.

The use of binary zeotropic mixtures with optimized composition leads to a gain in exergy efficiency of ii.8 percentage points (+3.three% of ORC net power target). The well-nigh efficient solution employs a mixture of isobutane/isopentane (0.66/0.34) with a supercritical regenerated ORC. The efficiency gain compared to the pure fluids is mainly due to the temperature glide occurring in condensation.

The technoeconomic optimization, performed for RE347mcc, R1336mzz, and the mixture of isobutane/isopentane, shows that RE347mcc is the best selection for low electricity prices (in absence of incentives). Its optimized ORC maintains skillful efficiency (generating 88% of the target mass catamenia rate of ORC vapor) as the electricity revenues more than than compensate for the equipment costs. Equally a comparison, the optimized cycle using R1336mzz has an appreciable reduction of ORC mass menstruum rate compared to the target value (it generates only 72% of the target mass menses rate). The main reason appears to be the compression point at the evaporator (due to larger enthalpy of evaporation of R1336mzz compared to RE347mcc) that limits the mass menstruation charge per unit. Some other of import event is the economic advantage of using the regenerator to preheat the liquid in place of the economizers (which would recover heat from H1 and H2). This is due to the higher heat transfer coefficient of organic fluids compared to stream H1 and H2 (air). For loftier electricity prices, the economic optimum becomes close to the thermodynamic optimum in terms of free energy performance and working fluid mass flow rates. Differences betwixt economic functioning of the different fluids are mainly due to the cost of the heat exchangers, favoring the fluid (RE347mcc) with larger regenerator.

The mixture results showed to be economically advantageous only for high electricity prices, although the relative difference compared to RE347mcc is pocket-size. The gain can likely not compensate for the extra equipment costs related to fluid flammability (i.east., need of a thermal oil loop) and to prevent fluid leakages (important consequence for zeotropic mixtures), non considered in this work.

As far as fluid selection criteria are concerned, this piece of work has shown that the thermodynamic performance of ORCs mainly depend on the disquisitional temperature of the fluids while the economic performance is influenced also by other parameters, such as the de-superheating rut (available for the regenerator) and the evaporation enthalpy (influencing the heat integration with the available hot streams and the raised mass period charge per unit of working fluid).

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the inquiry was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Astolfi, M., Martelli, Eastward., and Pierobon, L. (2017). "Thermodynamic and technoeconomic optimization of organic rankine cycle systems," in Organic Rankine Cycle (ORC) Power Systems, eds Eastward. Macchi and K. Astolfi (Woodhead Publishing), 173–249. doi: x.1016/B978-0-08-100510-1.00007-seven

CrossRef Full Text | Google Scholar

Azzolin, M., Berto, A., Bortolin, S., and Del Col, D. (2017). Heat transfer deposition during condensation of non-azeotropic mixtures. J. Phys. Conf. Ser. 923:012017. doi: 10.1088/1742-6596/923/one/012017

CrossRef Full Text | Google Scholar

Azzolin, One thousand., Bortolin, S., and Del Col, D. (2016). Predicting methods for menses boiling rut transfer of a non-azeotropic mixture within a single microchannel. Oestrus Transfer Eng. 37, 1136–1147. doi: 10.1080/01457632.2015.1111114

CrossRef Full Text | Google Scholar

Braimakis, Chiliad., Preißinger, One thousand., Brüggemann, D., Karellas, Due south., and Panopoulos, K. (2015). Low grade waste oestrus recovery with subcritical and supercritical Organic Rankine Wheel based on natural refrigerants and their binary mixtures. Energy 88, 80–92. doi: x.1016/j.energy.2015.03.092

CrossRef Full Text | Google Scholar

Campana, F., Bianchi, M., Branchini, L., De Pascale, A., Peretto, A., Baresi, Thou., et al. (2013). ORC waste oestrus recovery in European energy intensive industries: energy and GHG savings. Energ. Convers. Manage. 76, 244–252. doi: ten.1016/j.enconman.2013.07.041

CrossRef Full Text | Google Scholar

Cavallini, A. (2017). "Heat transfer and rut exchangers," in Organic Rankine Cycle (ORC) Ability Systems, eds E. Macchi and G. Astolfi (Woodhead Publishing), 397–470. doi: x.1016/B978-0-08-100510-1.00013-ii

CrossRef Full Text | Google Scholar

Chen, C.-L., Li, P.-Y., and Le, Due south. Due north. T. (2016). Organic Rankine cycle for waste heat recovery in a refinery. Ind. Eng. Chem. Res. 55, 3262–3275. doi: 10.1021/acs.iecr.5b03381

CrossRef Full Text | Google Scholar

Chys, Grand., van den Broek, M., Vanslambrouck, B., and De Paepe, G. (2012). Potential of zeotropic mixtures equally working fluids in organic Rankine cycles. Free energy 44, 623–632. doi: ten.1016/j.energy.2012.05.030

CrossRef Full Text | Google Scholar

Desai, Due north. B., and Bandyopadhyay, S. (2009). Process integration of organic Rankine cycle. Energy, 1674–1686. doi: 10.1016/j.energy.2009.04.037

CrossRef Total Text | Google Scholar

Duran, M. A., and Grossmann, I. E. (1986). Simultaneous optimization and rut integration of chemical processes. AICHE J. 32, 123–138. doi: 10.1002/aic.690320114

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. E. (2018). A bilevel decomposition method for the simultaneous synthesis of utility systems, Rankine cycles and heat exchanger networks. Comput. Aided Chem. Eng. 43, 373–378. doi: x.1016/B978-0-444-64235-half-dozen.50068-1

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. East. (in printing). A bilevel decomposition method for the simultaneous heat integration synthesis of steam/Organic Rankine Cycles. Comput. Chem. Eng. doi: x.1016/j.compchemeng.2019.05.041

CrossRef Total Text | Google Scholar

Elsido, C., Martelli, E., and Kreutz, T. (2019). Heat integration and rut recovery steam cycle optimization for a low-carbon lignite/biomass-to-jet fuel sit-in project. Appl. Energy 239, 1322–1342. doi: 10.1016/j.apenergy.2019.01.221

CrossRef Full Text | Google Scholar

Elsido, C., Mian, A., Marechal, F., and Martelli, E. (2017b). A general superstructure for the optimal synthesis and design of ability and inverse Rankine cycles. Comput. Aided Chem. Eng. 40, 2407–2412. doi: x.1016/B978-0-444-63965-3.50403-vii

CrossRef Full Text | Google Scholar

Elsido, C., Mian, A., and Martelli, Due east. (2017a). A systematic methodology for the techno-economic optimization of Organic Rankine Cycles. Free energy Procedia 129, 26–33. doi: ten.1016/j.egypro.2017.09.171

CrossRef Full Text | Google Scholar

E. P. R. Found (1993). Technical Assessment Guide (TAG) Electricity Supply, TR-102276-V1R7. Palo Alto, CA: EPRI.

Google Scholar

Hipólito-Valencia, B. J., Rubio-Castro, E., Ponce-Ortega, J. Yard., Serna-González, One thousand., Nápoles-Rivera, F., and El-Halwagi, G. M. (2013). Optimal integration of organic Rankine cycles with industrial processes. Energ. Convers. Manage. 73, 285–302. doi: 10.1016/j.enconman.2013.04.036

CrossRef Full Text | Google Scholar

IEA and Nordicetp (2016). Nordic Free energy Engineering Perspective 2016, ODEC/IEA. Oslo: Nordic Energy Research.

Google Scholar

Invernizzi, C. Chiliad. (2013). "Closed power cycle," in Thermodynamic Fundamentals and Applications (Brescia: Springer). 109–111.

Google Scholar

Invernizzi, C. M., Iora, P., Bonalumi, D., Macchi, E., Roberto, R., and Caldera, Grand. (2016). Titanium tetrachloride as novel working fluid for high temperature Rankine cycles: thermodynamic assay and experimental assessment of the thermal stability. Appl. Therm. Eng. 107, 21–27. doi: 10.1016/j.applthermaleng.2016.06.136

CrossRef Full Text | Google Scholar

Kalitventzeff, B., and Maréchal, F. (1999). Targetting the optimal integration of stram networks: mathematical tools and methodology. Comput. Chem. Eng. 23, S133–S136. doi: 10.1016/S0098-1354(99)80034-nine

CrossRef Full Text | Google Scholar

Karellas, S., Leontaritis, A. D., Panousis, G., Bellos, East., and Kakaras, E. (2013). Energetic and exergetic analysis of waste heat recovery systems in the cement industry. Free energy 58, 147–156. doi: 10.1016/j.energy.2013.03.097

CrossRef Full Text | Google Scholar

Kemp, I. C. (2006). Pinch Analysis and Process Integration, 2nd Edn. Abingdon: Butterworth-Heinemann, 15–36.

Google Scholar

Kruse, H., and Rinne, F. (1992). "Functioning and leakage investigations of refrigeration and airconditioning systems using refrigerant mixtures as working fluids," in International Refrigeration and Air conditioning Conference (Westward Lafayette, IN) 621–thirty.

Google Scholar

Ladam, Y., Solheim, A., Segatz, Yard., and Lorentsen, O. (2011). Heat recovery from aluminium reduction cells. Light Metals 2011, 393–398. doi: 10.1002/9781118061992.ch70

CrossRef Total Text | Google Scholar

Lampe, M., Stavrou, M., Bücker, M., Gross, J., and Bardow, A. (2014). Simultaneous optimization of working fluid and procedure for organic Rankine cycles (ORCs) using PC-SAFT. Ind. Eng. Chem. Res. 53, 8821–8830. doi: 10.1021/ie5006542

CrossRef Total Text | Google Scholar

Lemmon, E. W., Huber, M. 50., and McLinden, Chiliad. L. (2013). NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Send Properties-REFPROP. Version 9.1. National Found of Standards and Technology.

Google Scholar

Lemmon, Eastward. W., and McLinden, Chiliad. O. (2001). Method for Estimating Mixture Equation of State Parameters. National Establish of Standards and Engineering science.

Google Scholar

Linke, P., Papadopoulos, A., and Seferlis, P. (2015). Systematic methods for working fluid pick and the blueprint, integration and command of organic Rankine cycles-A review. Energies 8, 4755–4801. doi: 10.3390/en8064755

CrossRef Full Text | Google Scholar

Linnhoff, B. (1979). Themrodynamic analysis in the design of procedure networks, Ph.D. Thesis. Leeds: The Academy of Leedss.

Google Scholar

Martelli, East., and Amaldi, Due east. (2013). PGS-COM: a hybrid method for constrained non-smooth black-box optimization problems. Cursory review, novel algorithm and comparative evaluation. Comput. Chem. Eng. 63, 108–139. doi: ten.1016/j.compchemeng.2013.12.014

CrossRef Full Text | Google Scholar

Martelli, E., Capra, F., and Consonni, S. (2015). Numerical optimization of combined estrus and power Organic Rankine Cycles-Role A: design optimization. Energy 90, 310–328. doi: 10.1016/j.energy.2015.06.111

CrossRef Total Text | Google Scholar

Martelli, E., Elsido, C., Mian, A., and Marechal, F. (2016). Synthesis of oestrus exchanger networks and utility systems: Sequential initialization procedure and simultaneous MINLP algorithm. Comput. Aided Chem. Eng. 38, 1450–1454. doi: 10.1016/B978-0-444-63428-3.50246-0

CrossRef Full Text | Google Scholar

Martelli, Eastward., Elsido, C., Mian, A., and Marechal, F. (2017). MINLP model and two-stage algorithm for the simultaneous synthesis of heat exchanger networks, utility systems and heat recovery cycles. Comput. Chem. Eng. 106, 663–689. doi: 10.1016/j.compchemeng.2017.01.043

CrossRef Full Text | Google Scholar

Palma-Flores, O., Flores-Tlacuahuac, A., and Canseco-Melchor, G. (2014). Optimal molecular design of working fluids for sustainable low-temperature energy recovery. Comput. Chem. Eng. 72, 334–339. doi: ten.1016/j.compchemeng.2014.04.009

CrossRef Full Text | Google Scholar

Papadopoulos, A., Stijepovic, M., and Linke, P. (2010). On the systematic design and option of optimal working fluids for organic Rankine cycles. Appl. Therm. Eng. 30, 760–769. doi: 10.1016/j.applthermaleng.2009.12.006

CrossRef Full Text | Google Scholar

Sami, Due south. M. (2010). Energy and exergy assay of new refrigerant mixtures in an organic Rankine bike for depression temperature power generation. Int. J. Ambience Energy. 31, 23–32. doi: 10.1080/01430750.2010.9675805

CrossRef Full Text | Google Scholar

Scaccabarozzi, R., Tavano, M., Invernizzi, C. M., and Martelli, E. (2018). Comparison of working fluids and cycle optimization for heat recovery ORCs from large internal combustion enegines. Energy 158, 396–416. doi: 10.1016/j.energy.2018.06.017

CrossRef Total Text | Google Scholar

Solheim, A. (2018). Inert anodes-The bullheaded alley to environmental friendliness? in TMS 2018. Lite Metals 2018, 1253–1260. doi: 10.1007/978-3-319-72284-9_164

CrossRef Total Text | Google Scholar

Wang, E., Zhang, H., Fan, B., Ouyang, Yard., Zhao, Y., and Mu, Q. (2011). Study of working fluid option of organic Rankine cycle (ORC) for engine waste matter rut recovery. Free energy 36, 3406–3418. doi: 10.1016/j.energy.2011.03.041

CrossRef Total Text | Google Scholar

Yang, M., Zhang, H., Wang, E., Song, S., Bei, C., Chang, Y., et al. (2014). Report on mixed working fluids with different compositions in Organic Rankine Wheel (ORC) systems for vehicle diesel engines. Entropy 16, 4769–4787. doi: ten.3390/e16094769

CrossRef Total Text | Google Scholar

Yee, T., and Grossmann, I. (1990). Simultaneous optimization models for heat integration-Two. Estrus exchanger network synthesis. Comput. Chem. Eng. 14, 1165–1184. doi: 10.1016/0098-1354(90)85010-8

CrossRef Full Text | Google Scholar

Yu, H., Eason, J., Biegler, 50. T., and Feng, 10. (2017). Simultaneous heat integration and techno-economic optimization of Organic Rankine Cycle (ORC) for multiple waste matter heat stream recovery. Energy, 322–33. doi: ten.1016/j.energy.2016.12.061

CrossRef Full Text | Google Scholar

Yu, M., Gudjonsdottir, G. S., Valdimarsson, P., and Saevarsdottir, G. (2018). Waste oestrus recovery from aluminum production. Miner. Met. Mater. Ser. Fvi, 165–178. doi: 10.1007/978-three-319-72362-4_14

CrossRef Total Text | Google Scholar

Zhang, J., Zhang, H., Yang, Thou., Yang, F., Wang, Z., Zhao, Yard., et al. (2014). Performance analysis of regenerative organic Rankine bike (RORC) the pure working fluid and the zeotropic mixture over the whole using operating range of a diesel engine. Energ. Convers. Manage. 84, 282–294. doi: ten.1016/j.enconman.2014.04.036

CrossRef Full Text | Google Scholar

Zhang, L. H., Wu, L. J., Hu, H. R., and Gao, X. J. (2013). Comparison and optimization of low temperature flue gas power generation systems in iron and steel enterprises. Reneng Dongli Gongcheng/J. Eng. Therm. Energy Power 28, 257–261.

Google Scholar

Appendix

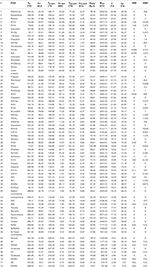
Table A1. Thermodynamic optimization results of all pure fluids ranked according to the exergy efficiency.

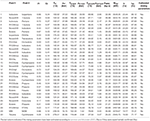
Table A2. Thermodynamic optimization results of all mixtures ranked according to the exergy efficiency.

archibaldasaints.blogspot.com

Source: https://www.frontiersin.org/articles/10.3389/fenrg.2019.00044/full

Share this post